Overview
The D’Hondt formula stands as a pivotal mathematical method in proportional representation electoral systems, designed to allocate legislative seats in accordance with the votes garnered by political groups. This approach ensures that the distribution of seats accurately mirrors the overall vote share, thereby enhancing fairness in representation.
By dividing total votes by a series of divisors, the formula generates quotients that are subsequently ranked for seat assignment. This systematic process not only promotes equity but also offers a stark contrast to majority or plurality systems, which often lead to disproportionate representation.
Introduction
The D’Hondt formula is a cornerstone of proportional representation in electoral systems, fundamentally transforming how votes translate into legislative power. By employing a systematic approach to seat allocation, this formula enhances fairness in representation while addressing the complexities of diverse political landscapes.
However, as nations increasingly adopt this method, questions arise:
- Does the D’Hondt formula truly balance the scales between larger parties and smaller factions, or
- Does it inadvertently perpetuate disparities in representation?
Exploring the intricacies of this mathematical tool reveals both its historical significance and its implications for modern governance.
Define the D’Hondt Formula and Its Purpose
The D’Hondt formula, widely recognized as the greatest divisors technique, is an essential mathematical tool in proportional representation electoral systems for allocating legislative seats. Its primary objective is to convert the vote counts received by political groups into a corresponding number of seats through the D’Hondt formula, thereby ensuring that the distribution of seats mirrors the overall vote share of each group. This method significantly enhances fairness and representation within democratic frameworks. By using the D’Hondt formula, the total votes received by each group are divided by a series of divisors (1, 2, 3, etc.). The D’Hondt formula generates quotients that are then used to allocate positions based on the highest values.
Furthermore, this approach not only promotes equitable representation but also addresses the discrepancies often seen in majority or plurality systems. In such systems, groups may secure more seats despite receiving fewer votes, as evidenced by historical elections in the UK, notably those in 1951 and February 1974. Moreover, the proportional representation model has gained traction in numerous countries, with approximately two-thirds of the world’s democratic lawmakers elected through such systems. Critics of proportional representation contend that it may lead to the emergence of splinter parties, potentially resulting in fragile and unstable governments.
As highlighted by Anthony Fowler, the D’Hondt formula calculates the average by dividing the number of votes by the number of seats plus one, underscoring its systematic approach to seat allocation. Ultimately, the proportional representation system plays a pivotal role in ensuring that commensurate with their electoral support, thereby bolstering the legitimacy of governmental decisions.
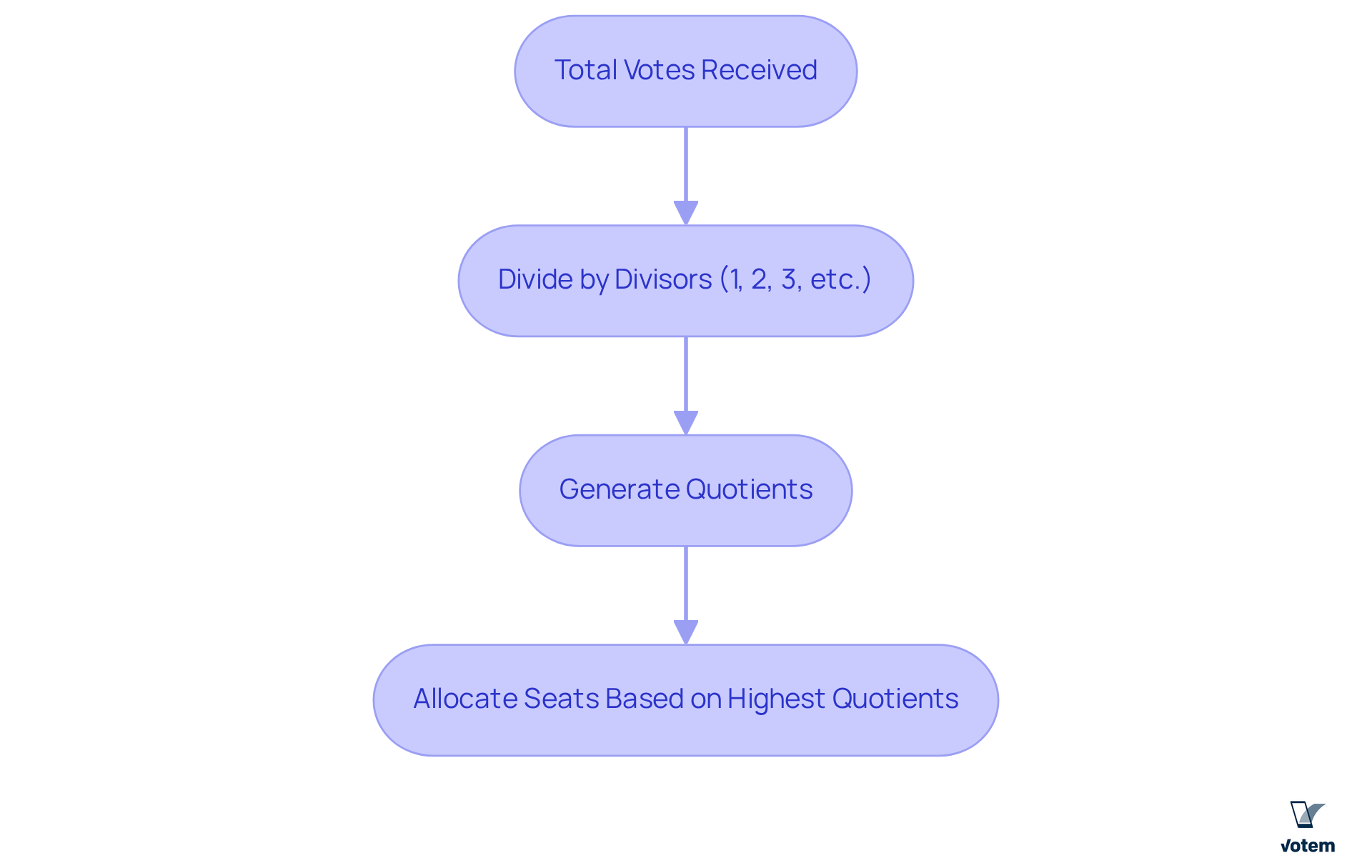
Explore the Historical Context and Development of the D’Hondt Formula
The formula developed by Belgian lawyer Victor in 1882 emerged during a pivotal era in Belgium’s political landscape, characterized by the necessity to represent diverse linguistic and political groups within the parliament. This formula aimed to create a more , effectively reflecting the nation’s multifaceted political environment. Its design not only addressed the immediate representation needs but also laid the foundation for a more inclusive electoral process.
Over the years, the d’hondt formula has gained global traction as an electoral system, being implemented in 36 nations, including Belgium, Brazil, and Spain, thereby establishing itself as a cornerstone for proportional representation in legislative elections. The historical significance of the d’hondt formula is highlighted by its ability to enhance democratic representation in increasingly complex political contexts, ensuring that both larger and smaller groups can secure their rightful place in governance.
As Victor articulated, “By employing a straightforward mathematical algorithm, the approach divides the number of votes garnered by each group by a series of divisors, thus enabling smaller factions to obtain representation.” Furthermore, this method reduces vote wastage compared to first-past-the-post systems, slightly favoring larger groups while still allowing smaller groups to achieve legislative seats.
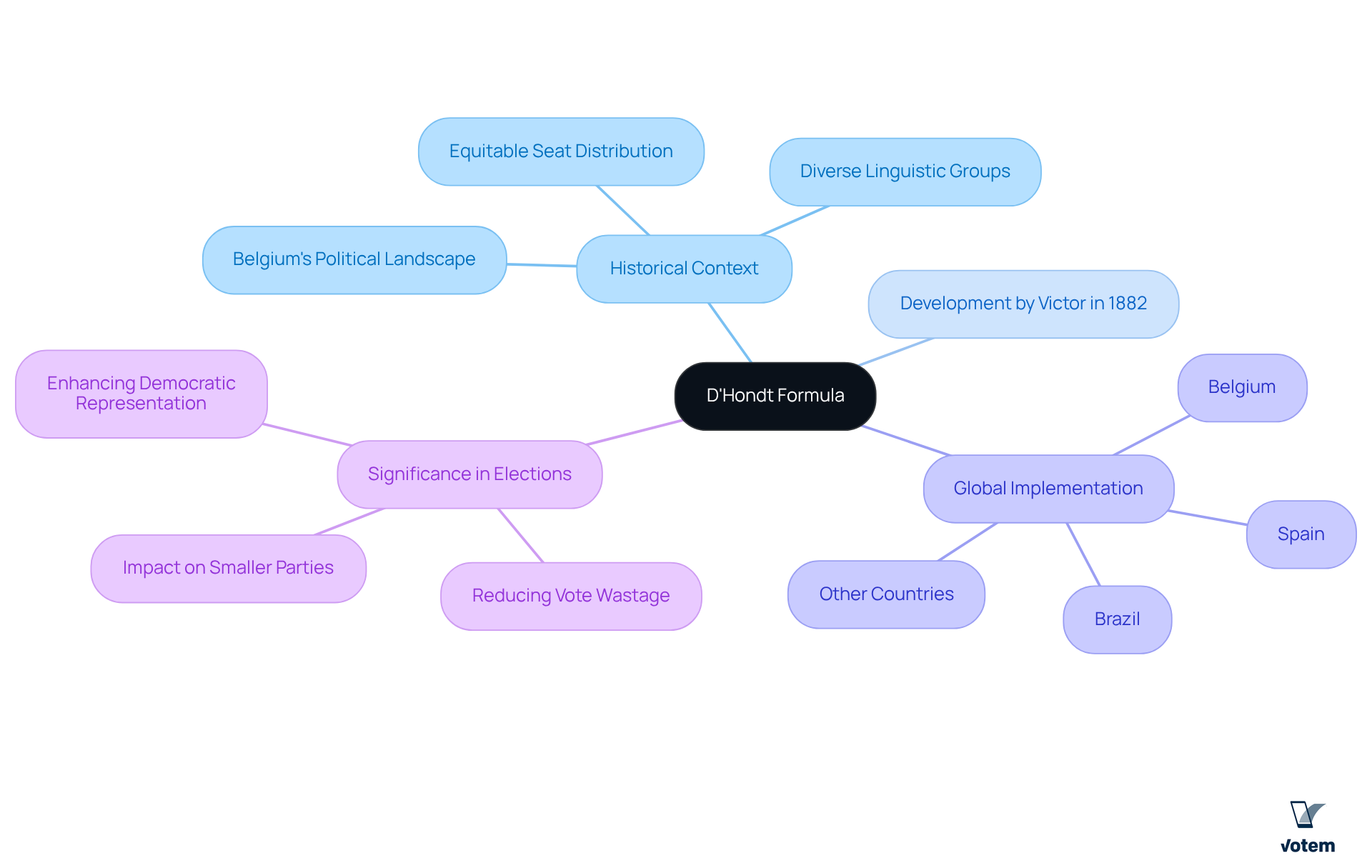
Analyze the Mechanics and Key Characteristics of the D’Hondt Formula
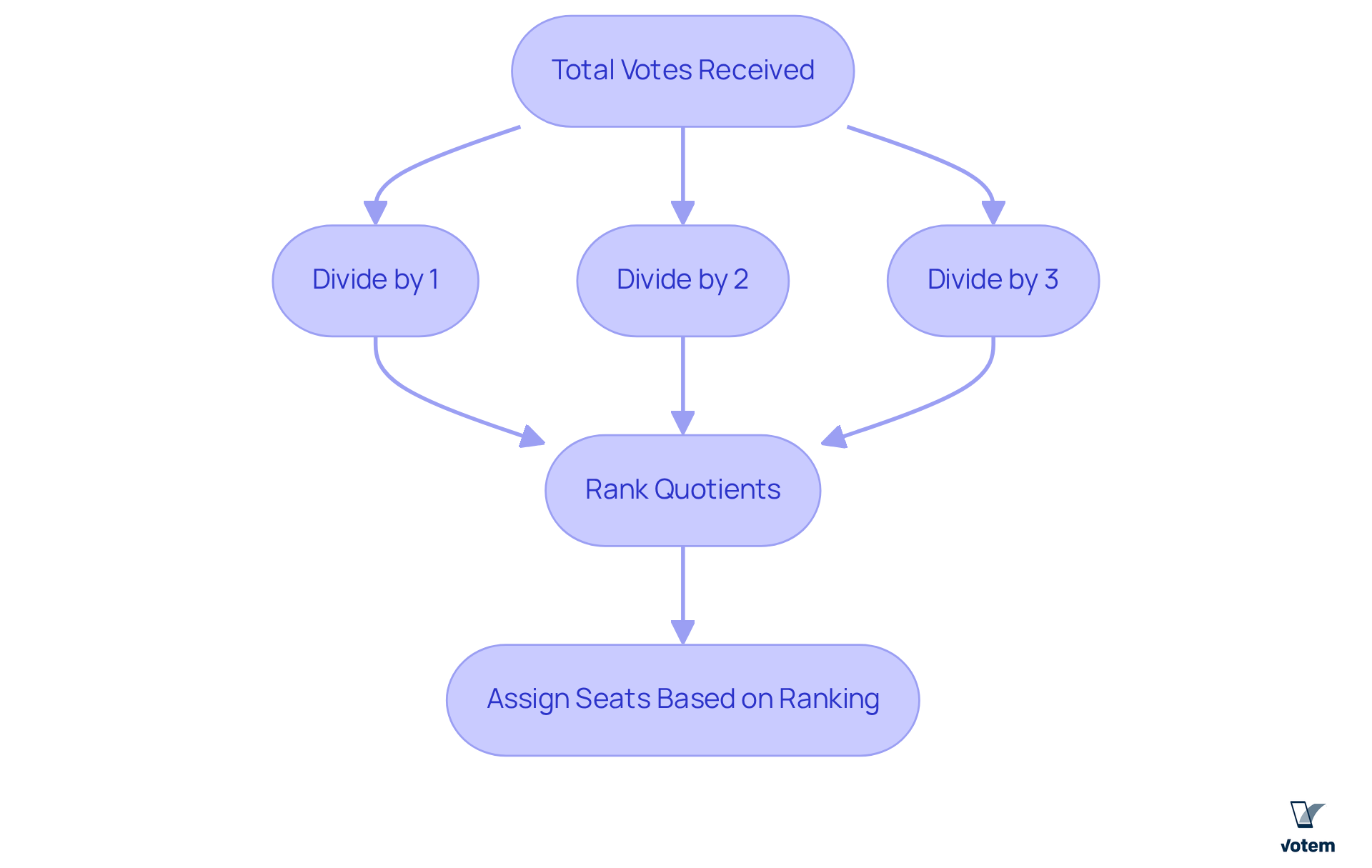
The mechanics of the d’hondt formula involve a straightforward process in which the total votes received by each group are divided by a series of divisors. For instance, if a group garners 100,000 votes, the quotients are calculated as follows:
- 100,000 (divided by 1)
- 50,000 (divided by 2)
- 33,333 (divided by 3)
and so forth. These resulting quotients are then ranked from highest to lowest, with seats assigned to the groups that hold the highest quotients until all available seats are filled. This electoral system is notable for its simplicity, transparency, and tendency to favor larger parties, which can contribute to a more stable government, albeit at the potential cost of underrepresentation for smaller parties. This delicate balance between representation and governability is a critical aspect of the design of the d’hondt formula.
Furthermore, the d’hondt formula is employed in 15 EU Member States for elections to the European Parliament, underscoring its significance across various electoral systems. For example, consider a recent election scenario where Party A received 300 votes, Party B 210 votes, and Party C 120 votes in the first round. Party A would secure the first position, and in the subsequent round, its votes would be halved, resulting in a new quotient of 150. Concurrently, Party B’s votes would also be divided by two after securing its initial position, yielding a quotient of 105. This iterative process continues until all seats are allocated, effectively illustrating the in electoral contexts. As Victor d’Hondt noted, this approach was devised to more effectively cater to diverse political traditions, ensuring an equitable allocation of power among groups.
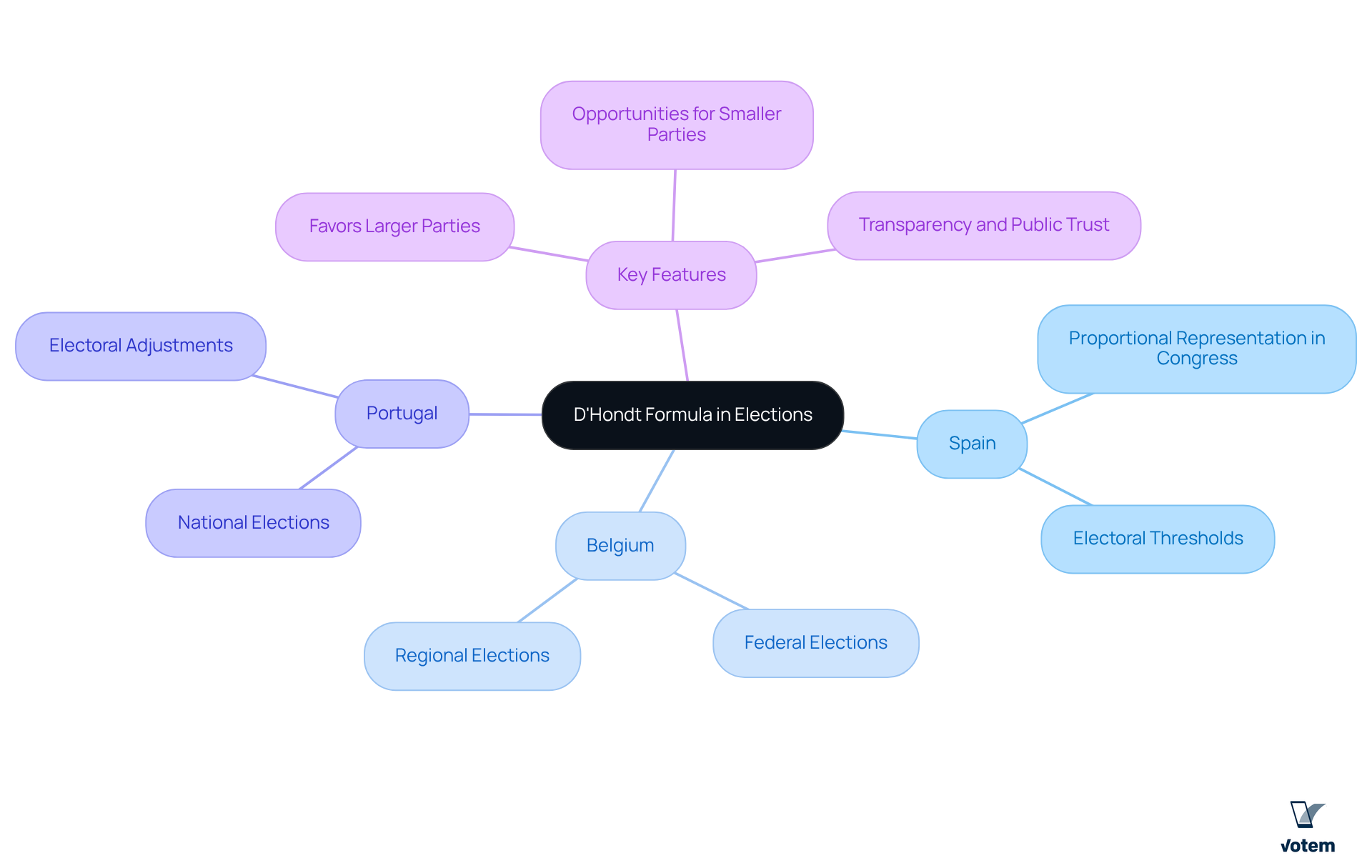
Examine Applications and Variations of the D’Hondt Formula in Elections
The d’hondt formula serves as a pivotal approach within electoral systems across the globe, particularly evident in national and regional elections in countries such as Belgium, Spain, and Portugal. Its application varies significantly depending on the electoral landscape, including the number of available positions and the electoral thresholds that parties must meet to secure representation.
For example, in Spain, the d’hondt formula is used as a proportional representation system to allocate positions in the Congress of Deputies, whereas Belgium utilizes it for both federal and regional elections. Variations of the may include adjustments to the divisor series or the introduction of electoral thresholds designed to enhance proportionality.
These modifications reflect ongoing efforts to refine electoral systems and improve representation, underscoring the formula’s essential role in promoting democratic governance. Furthermore, while the d’hondt formula tends to favor larger parties, it simultaneously provides opportunities for smaller parties to obtain seats, thereby fostering a balanced representation framework.
Conclusion
The D’Hondt formula is a pivotal mechanism for ensuring proportional representation in electoral systems, effectively translating vote counts into legislative seats. This mathematical approach not only enhances fairness within democratic frameworks but also addresses the inherent disparities often found in majority or plurality systems. By employing a systematic method of dividing total votes by a series of divisors, the D’Hondt formula guarantees that the distribution of seats closely aligns with the overall vote share of each political group, thus fortifying the legitimacy of governance.
Throughout this article, we have explored key insights into the D’Hondt formula’s historical context, mechanics, and applications. Originating from Belgium in the late 19th century, the formula has evolved into a widely adopted electoral system utilized in various countries around the world. Its straightforward process of calculating quotients from vote counts ensures that both larger and smaller parties can secure representation, thereby contributing to a balanced legislative landscape. Furthermore, the formula’s adaptability through variations in divisor series and electoral thresholds reflects ongoing efforts to refine electoral practices and enhance democratic governance.
In summary, the D’Hondt formula plays a crucial role in shaping electoral outcomes and promoting equitable representation. As democratic societies navigate complex political landscapes, understanding and applying such proportional representation methods remain essential. Advocating for the implementation of the D’Hondt formula in electoral systems can lead to a more inclusive and representative governance structure, ultimately empowering diverse voices within the political arena.
Frequently Asked Questions
What is the D’Hondt formula?
The D’Hondt formula, also known as the greatest divisors technique, is a mathematical tool used in proportional representation electoral systems to allocate legislative seats based on the vote counts received by political groups.
What is the purpose of the D’Hondt formula?
The primary purpose of the D’Hondt formula is to convert the vote counts of political groups into a corresponding number of seats, ensuring that the distribution of seats reflects the overall vote share of each group to enhance fairness and representation in democratic systems.
How does the D’Hondt formula work?
The D’Hondt formula works by dividing the total votes received by each group by a series of divisors (1, 2, 3, etc.) to generate quotients, which are then used to allocate seats based on the highest values.
What are the advantages of using the D’Hondt formula?
The D’Hondt formula promotes equitable representation and addresses discrepancies seen in majority or plurality systems, where groups may gain more seats than their vote counts justify.
What criticisms exist regarding proportional representation systems like the D’Hondt formula?
Critics argue that proportional representation systems may lead to the emergence of splinter parties, which can result in fragile and unstable governments.
How widespread is the use of the D’Hondt formula in the world?
Approximately two-thirds of the world’s democratic lawmakers are elected through proportional representation systems, which often utilize the D’Hondt formula.
What is the significance of the D’Hondt formula in representing minority groups?
The D’Hondt formula plays a crucial role in ensuring that minority groups receive representation that corresponds to their electoral support, thus enhancing the legitimacy of governmental decisions.
List of Sources
- Define the D’Hondt Formula and Its Purpose
- D’Hondt formula | politics | Britannica (https://britannica.com/topic/dHondt-formula)
- effectivegov.uchicago.edu (https://effectivegov.uchicago.edu/primers/proportional-representation)
- Explore the Historical Context and Development of the D’Hondt Formula
- Victor d’Hondt, the dead Belgian who could influence the European elections (https://theguardian.com/politics/shortcuts/2019/may/22/victor-dhondt-the-dead-belgian-who-could-influence-the-european-elections)
- d’Hondt system – The Penguin Companion to European Union (https://penguincompaniontoeu.com/additional_entries/dhondt-system)
- Understanding the D’Hondt Method in modern elections (https://eligovoting.com/understanding-the-dhondt-method)
- D’Hondt method – Wikipedia (https://en.wikipedia.org/wiki/D’Hondt_method)
- Understanding the D’Hondt Method: Its Use in the Northern Ireland Assembly (https://niassembly.gov.uk/news-and-media/assembly-explained/understanding-the-dhondt-method-its-use-in-the-northern-ireland-assembly)
- Analyze the Mechanics and Key Characteristics of the D’Hondt Formula
- Senedd election 2026: What is the D’Hondt formula and how does it work? (https://senedd.wales/senedd-now/senedd-blog/senedd-election-2026-what-is-the-d-hondt-formula-and-how-does-it-work)
- 2019 European Elections: How does the voting system work? (https://bbc.com/news/uk-politics-27187434)
- Understanding the D’Hondt Method: Its Use in the Northern Ireland Assembly (https://niassembly.gov.uk/news-and-media/assembly-explained/understanding-the-dhondt-method-its-use-in-the-northern-ireland-assembly)
- Understanding the d’Hondt method: Allocation of parliamentary seats and leadership positions | Think Tank | European Parliament (https://europarl.europa.eu/thinktank/en/document/EPRS_BRI(2024)762352)
- Examine Applications and Variations of the D’Hondt Formula in Elections
- EU elections voting system explained: D’Hondt worry – UK in a changing Europe (https://ukandeu.ac.uk/eu-elections-voting-system-explained-dhondt-worry)
- 2019 European Elections: How does the voting system work? (https://bbc.com/news/uk-politics-27187434)
- D’Hondt system for picking NI ministers in Stormont (https://bbc.com/news/uk-northern-ireland-politics-13359731)
- Understanding the D’Hondt Method in modern elections (https://eligovoting.com/understanding-the-dhondt-method)
- Understanding the D’Hondt Method: Its Use in the Northern Ireland Assembly (https://niassembly.gov.uk/news-and-media/assembly-explained/understanding-the-dhondt-method-its-use-in-the-northern-ireland-assembly)

